Notícias

Descobertas sobre o calor
A recente demonstração de que o calor pode ser transmitido através do vácuo em nanoescala causou alvoroço, mas parece que as surpresas envolvendo o calor não param por aí.
Pesquisadores suíços desenvolveram um novo modelo que descreve como o calor se espalha no interior dos materiais cristalinos que se mostrou capaz de explicar porque, em algumas condições, o calor se propaga nos sólidos como se fosse um líquido, fugindo do padrão geral da difusão.
O trabalho tem grande interesse prático porque as novas equações facilitarão o projeto de componentes eletrônicos de próxima geração, fabricados em nanoescala, nos quais esses fenômenos se tornam predominantes.
É o caso, por exemplo, dos materiais à base de carbono, como grafeno, grafite ou diamante, nos quais os fenômenos hidrodinâmicos são predominantes.
O superaquecimento é o principal fator limitante da miniaturização e do pretendido aumento de eficiência dos componentes eletrônicos. Assim, para maximizar a eficiência e prever se um componente funcionará - ou simplesmente derreterá - é crucial ter o modelo certo.

Formas de transmissão do calor
A conhecida equação do calor de Fourier descreve como as temperaturas mudam no espaço e no tempo quando o calor flui em um material sólido. A formulação foi desenvolvida em 1822 por Joseph Fourier, um matemático e físico francês contratado por Napoleão para aumentar a taxa de repetição dos tiros de canhão, que era limitada pelo superaquecimento.
Continua depois da publicidade |
A equação de Fourier funciona bem para descrever a condução em objetos macroscópicos (dos milímetros para cima) e em altas temperaturas, mas não descreve a propagação hidrodinâmica do calor, que pode aparecer em componentes eletrônicos contendo materiais como grafite e grafeno.
Um desses fenômenos de propagação de calor é conhecido como fluxo de calor de Poiseuille. É aqui que o calor se propaga dentro de um material como se fosse um fluxo de fluido viscoso. Outro fenômeno, chamado "segundo som", ocorre quando o calor se propaga em um cristal como uma onda, semelhante à maneira pela qual o som se espalha pelo ar.
Como esses fenômenos não são descritos pela equação de Fourier, até agora os pesquisadores os analisavam usando modelos microscópicos explícitos, como a equação de transporte de Boltzmann. No entanto, a complexidade desses modelos significa que eles não podem ser usados para projetar dispositivos eletrônicos complexos.
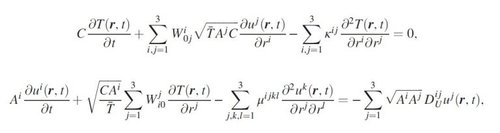
Equações do calor viscoso
Este problema foi resolvido agora por Michele Simoncelli e colegas da Escola Politécnica Federal de Lausanne, na Suíça. Eles mostraram como o calor proveniente das vibrações atômicas em um sólido pode ser descrito rigorosamente por duas novas "equações do calor viscoso", que estendem a lei de Fourier para cobrir qualquer propagação de calor que não seja difusiva.
"Essas equações de calor viscoso explicam por que e em quais condições a propagação de calor se torna mais parecida com um fluido do que difusa. Elas mostram que a condução do calor é governada não apenas pela condutividade térmica, conforme descrito pela lei de Fourier, mas também por um segundo parâmetro, a viscosidade térmica," explicou Simoncelli.
Os resultados são oportunos. Desde a década de 1960 até recentemente, os fenômenos hidrodinâmicos de calor só foram observados em temperaturas criogênicas (em torno de -260 ºC) e, portanto, eram considerados irrelevantes para as aplicações práticas. Já em 2015, a mesma equipe previu que isso seria muito diferente nos materiais bidimensionais e em camadas - uma previsão que foi confirmada com a publicação na Science de experimentos pioneiros que mostraram que o calor propaga-se em ondas no grafeno, seguindo o padrão agora conhecido como segundo som.
Mais importante, a formulação também prevê que a propagação de calor hidrodinâmico pode ocorrer a temperatura ambiente, dependendo do tamanho e do tipo de material.
Gostou? Então compartilhe:
