Notícias
- Material Didático
- Materiais - FundamentosParâmetros de Rede - Direções e Planos Cristalinos
- Direções Cristalinas
- Origem do sistema de coordenadas
- Escolha dos eixos coordenados
- Planos atômicos
- Porque os planos atômicos são importantes?
Direções Cristalinas
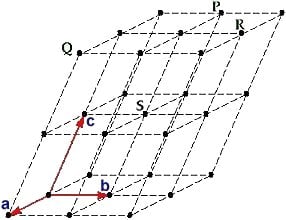
a, b e c definem os eixos de um sistema de coordenadas em 3D. Qualquer linha (ou direção) do sistema de coordenadas pode ser especificada através de dois pontos:
- um deles sempre é tomado como sendo a origem do sistema de coordenadas, (0,0,0) por convenção;
- o outro, é o primeiro ponto do cristal, (u,w,v), que você alcançaria caso estivesse andando na direção especificada a partir de (0,0,0).
Distinguir uma direção cristalina de um ponto do cristal é fácil, já que a direção é representada entre colchetes [...].
Origem do sistema de coordenadas
O espaço lático é infinito...
A escolha de uma origem é completamente arbitrária, uma vez que cada ponto do reticulado cristalino é idêntico.
A designação de pontos, direções e planos específicos fixados no espaço absoluto serão alterados caso a origem seja mudada, MAS... todas as designações serão auto-consistentes se partirem da origem como uma referência absoluta.
Exemplo: Dada uma origem qualquer, haverá sempre uma direção [110] definida univocamente, e [110] sempre fará exatamente o mesmo ângulo com a direção [100].
Escolha dos eixos coordenados
Sempre que possível, escolhe-se como sistema de referência o cartesiano (i.e., o sistema convencional de coordenadas x,y,z).
Porém, quando estamos lidando com cristais e suas propriedades, é melhor deixar o próprio reticulado espacial definir o sistema de coordenadas mais apropriado para ele, em função dos eixos cristalinos.
Os eixos podem não ser perpendiculares entre si, bem como as unidades para cada eixo, que podem ser diferentes (se os parâmetros de rede forem diferentes).
Planos atômicos
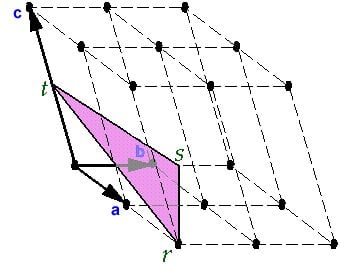
Considere a figura acima. As interseções do plano com os eixos são:
- eixo a em r = 2
- eixo b em s = 4/3
- eixo c em t = ½
Como podemos designar simbolicamente os planos de um reticulado?
- Calcule os recíprocos de r, s, e t;
- Ache o mínimo múltiplo comum que converte todos o recíprocos em inteiros;
- Inclua estes valores em parênteses.
Isto é chamado notação em Índice de Miller.
Desta forma, para o plano acima, temos o seguinte Índice de Miller: (2,3,8)
Veja os planos cristalinos interativamente.
Veja as direções cristalinas interativamente.
Porque os planos atômicos são importantes?
Para a determinação da estrutura cristalina
Os métodos de difração medem diretamente a distância entre planos paralelos de pontos do reticulado cristalino. Esta informação é usada para determinar os parâmetros do reticulado de um cristal.
Os métodos de difração também medem os ângulos entre os planos do reticulado. Estes são usados para determinar os ângulos interaxiais de um cristal.
Para a deformação plástica
A deformação plástica (permanente) dos metais ocorre pelo deslizamento dos átomos, escorregando uns sobre os outros no cristal. Este deslizamento tende a acontecer preferencialmente ao longo de planos e direções específicos do cristal.
Para as propriedades de transporte
Em certos materiais, a estrutura atômica em determinados planos causa o transporte de elétrons e/ou acelera a condução nestes planos, e, relativamente, reduz a velocidade em planos distantes destes.
Exemplo 1: Grafita
A condução de calor é mais rápida nos planos unidos covalentemente sp2 do que nas direções perpendiculares a esses planos.
Exemplo 2: supercondutores a base de YBa2Cu3O7
Alguns planos contêm somente Cu e O. Estes planos conduzem pares de elétrons (chamados pares de cobre) que são os responsáveis pela supercondutividade. Estes supercondutores são eletricamente isolantes em direções perpendiculares as dos planos Cu-O.
Gostou? Então compartilhe:
Notícias relacionadas
